Ridge Regression parameters

Overview:

Ridge regression is a powerful technique in machine learning used for regression tasks. It extends ordinary least squares regression by adding a penalty term to the cost function, which helps to mitigate the problem of overfitting. This penalty term, known as L2 regularization, penalizes the model for having large coefficients. Ridge regression is particularly useful when dealing with datasets that suffer from multicollinearity, where independent variables are highly correlated with each other.

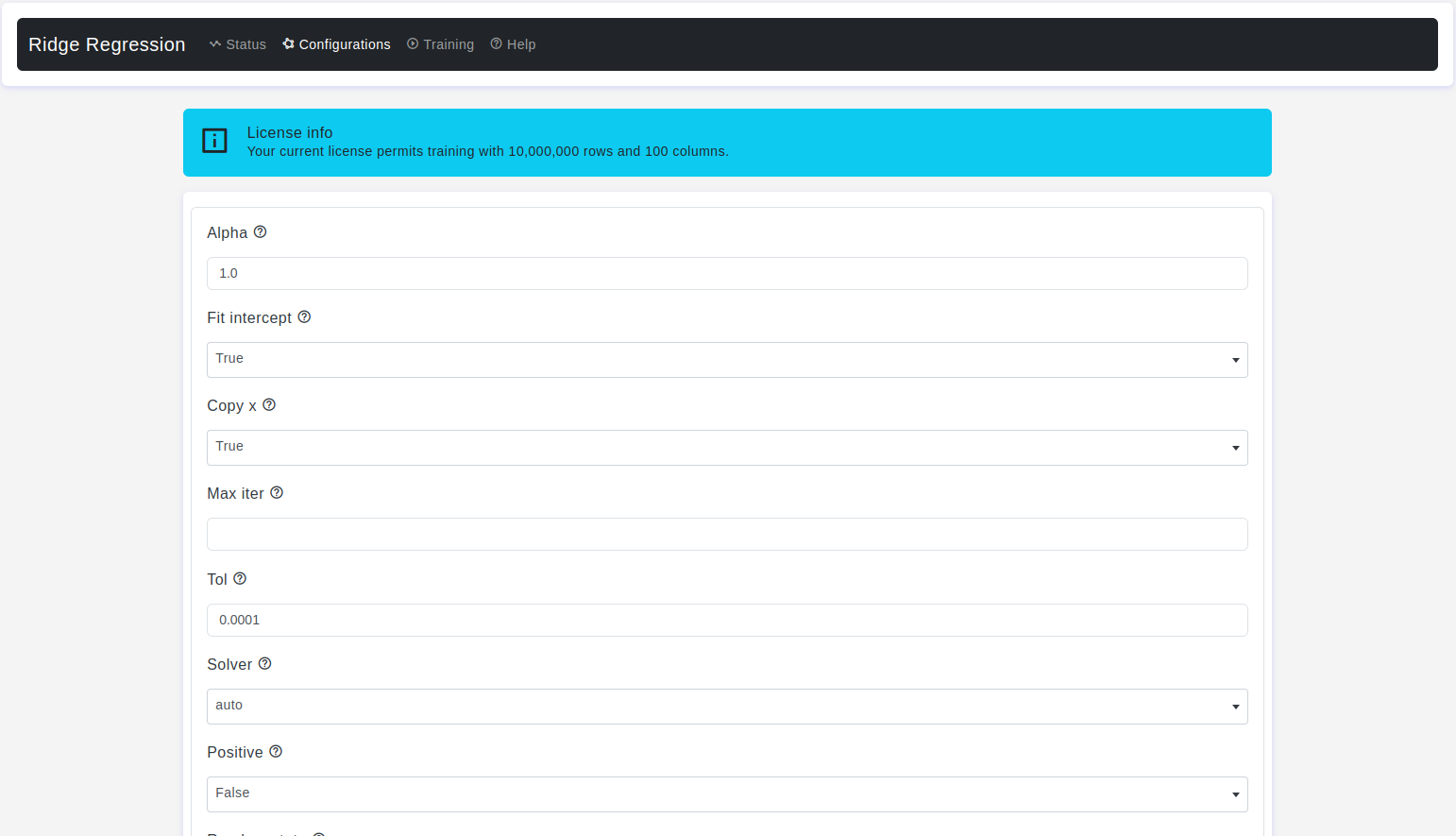
Configurations page:

The Configurations page allows users to adjust various parameters of the ridge regression model. Here are the details:

Alpha

• Default Value: 1.0
• Description: It refers to the regularization strength or regularization parameter. Ridge regression is a linear regression technique that includes L2 regularization to prevent overfitting by adding a penalty term to the linear regression cost function. The penalty term is proportional to the sum of the squares of the coefficients (slopes) of the independent variables.
• Warning: When alpha = 0, the objective is equivalent to ordinary least squares, solved by the LinearRegression. For numerical reasons, using alpha = 0 with the Ridge is not advised. Instead, you should use the LinearRegression.

Fit Intercept

• Default Value: True
• Description:  It is a boolean parameter that determines whether or not the model should include an intercept term (also known as the bias term) in the regression equation. This term represents the y-intercept of the linear equation and accounts for the value of the dependent variable (output) when all independent variables (input) are set to zero.

Copy X

• Default Value: True
• Description: It refers to whether a copy of the input data (the independent variables) should be made before fitting the model. This parameter is typically used in situations where you want to control whether the original input data is modified during the fitting process.

Max Iter

• Default Value: None
• Description: It controls the maximum number of iterations or optimization steps the algorithm is allowed to take while searching for the optimal coefficients.

Tol

• Default Value: 1e-4
• Description: The tol parameter (short for tolerance) is used to control the convergence criterion for the iterative optimization algorithm. The iterative optimization algorithm in Ridge regression is typically used to find the optimal values for the coefficients (weights) that minimize the cost function, which consists of the least squares loss and the L2 regularization term.

Solver

• Default Value: auto
• Description: It specifies the algorithm or method used to solve the optimization problem to find the optimal coefficients that minimize the Ridge regression cost function. The choice of solver affects how efficiently and accurately Ridge regression finds the best-fitting linear model with L2 regularization.
  • auto chooses the solver automatically based on the type of data.
  • svd uses a Singular Value Decomposition of input to compute the Ridge coefficients. It is the most stable solver, in particular more stable for singular matrices than cholesky at the cost of being slower.
  • cholesky This solver uses the Cholesky decomposition to directly compute the optimal coefficients. It is a good choice for datasets with a moderate number of features and is typically efficient for dense data.
  • sparse_cg This solver employs the Conjugate Gradient method to solve the Ridge regression optimization problem. It is particularly useful for large datasets with sparse features.
  • lsqr It is the fastest and uses an iterative procedure.
  • sagThis solver stands for Stochastic Average Gradient Descent. It is an iterative optimization algorithm that is efficient for large datasets, including those with a large number of features, and it supports both L1 and L2 regularization.
  • lbfgs It can be used only when positive is True.

Positive

• Default Value: False
• Description: It is a boolean parameter that determines whether or not the model should enforce that the coefficients (slopes) of the independent variables are strictly non-negative. Setting positive=True in Ridge regression ensures that all coefficient values are greater than or equal to zero, effectively constraining the linear relationship between the dependent variable and the independent variables to be positive.

Random State

• Default Value: None
• Description: It is used to control the randomness or randomness-related behavior of the algorithm when there are random elements involved, such as the shuffling of data or the initialization of coefficients.
• Warning: Used when solver = sag or saga to shuffle the data

Test Size

• Default Value: 0.2
• Description: The test size parameter is used when splitting the dataset into these subsets, and it specifies the portion of the data that will be used for testing.

Train Size

• Default Value: 0.8
• Description: The train size parameter is used when splitting the dataset into these subsets, and it specifies the portion of the data that will be used for model training.

Conclusion

Ridge regression is a valuable tool in the machine learning practitioner's toolkit, especially when dealing with datasets prone to overfitting or multicollinearity. By understanding and appropriately tuning its parameters, users can effectively leverage Ridge regression for building robust regression models.